Bei vielen mikroökonomischen Fragestellungen erweist sich ein mathematisches Hilfsmittel als ausgesprochen nützlich: die Ableitung. Nahezu jeder ist in der Lage, die erste Ableitung der Funktion

$$y = a{x^b} \tag{1}$$ $$y' = ba{x^{b - 1}} \tag{2}$$

anzugeben. Leider werden die Ableitungsregeln in der Schule wohl oft nur stur gepaukt, anstatt dass die Lehrerinnen und Lehrer den Schülerinnen und Schülern* deutlich machen, was inhaltlich dahinter steht.

Was man wissen sollte: Die Ableitung einer Funktion informiert über deren Steigung. Eine Gerade z.B. hat eine konstante Steigung. Deswegen liefert die Anwendung der obigen Regel einen konstanten Wert:

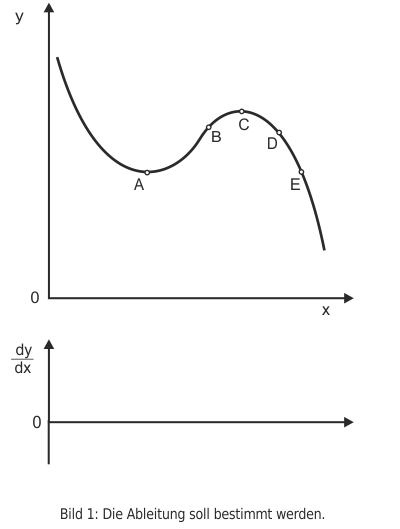
$$y = c + d \cdot {x^1} \tag{3}$$ $$y' = 0 + 1 \cdot d \cdot {x^{1 - 1}} = d \tag{4}$$

Die Funktion in Abbildung 1 ändert ihre Steigung laufend. Folglich ist die erste Ableitung vom jeweiligen x-Wert abhängig. Wenn wir den x-Wert für B in die erste Ableitung einsetzen, erhalten wir einen anderen Wert, als wenn wir den Wert für D einsetzen.

Aber auch ohne dass wir etwas berechnen, können wir durch die Methode des scharfen Hinsehens bereits erkennen, dass die Ableitung in B positiv, in D und E negativ und in A und C jeweils null sein muss.

Die maussensitive Abbildung 1 zeigt, wie sich grafisch die erste Ableitung für Punkt B konstruieren lässt. Die blaue Strecke (Bild 2) im oberen Diagramm ist die Zunahme des Ordinatenwertes, wenn sich der Abszissenwert um 1 erhöht (=Steigung). Sie wird in das untere Diagramm übertragen. Wenn man die Vorgehensweise für weitere Punkte wiederholt, erhält man die Funktion der ersten Ableitung (Bild 3) im unteren Teildiagramm. Das Berechnen der ersten Ableitung ist also nichts anderes als die wiederholte grafische Ermittlung der Steigung einer Funktion.

Daraus erkennt man, dass sich besondere Punkte der Funktion - nämlich Maxima und Minima - dadurch auszeichnen, dass die erste Ableitung den Wert null annimmt. Das kann man auch schärfer formulieren: Maxima und Minima setzen notwendig voraus, dass die erste Ableitung null ist. Leider ist die Steigung von null aber noch keine hinreichende Bedingung für das Vorliegen eines Extremwertes. Stellen Sie sich vor, Sie gingen einen Berg hinauf. Dann kann es ja ohne Weiteres sein, dass zwischendrin mal ein kleines waagerechtes Wegstück kommt, die Steigung anschließend aber sofort wieder positiv ist. Die Steigung kann also zwischendrin null sein, ohne dass man schon auf einem (lokalen) Gipfel stehen muss.

Die für Punkt B bestimmte Ableitung gilt nur "in einer kleinen Umgebung" von Punkt B, genau genommen gilt sie nur in B selbst. Aber für kleine ("marginale") Änderungen des $x$-Wertes ${\rm{d}}{\kern 1pt} x$ liefert uns die erste Ableitung durch die Berechnung von $y' \cdot {\rm{d}}{\kern 1pt} x$ (erste Ableitung für den aktuellen $x$-Wert mal Änderung des $x$-Wertes) eine gute Näherung für die zu erwartende Änderung des $y$-Wertes. Bei größeren Änderungen ist diese sogenannte Marginalanalyse wenn überhaupt, dann nur mit größter Vorsicht anwendbar [Beispiel].

Bei der Gelegenheit noch ein ceterum censeo: Die Mathematiker schreiben zur Kennzeichnung der Ableitung gerne einen Strich wie hier bei $y'$ in Gleichung (2). Warum eigentlich? Vielleicht weil es zeitsparend ist. Es lässt sich auch schnell sprechen: ipsilon Strich.

Viel schöner, weil aussagekräftiger, ist aber die Schreibweise als Bruch ${{{\rm{d}}{\kern 1pt} y} \over {{\rm{d}}{\kern 1pt} x}}$, gesprochen: de ipsilon nach de icks. Hier sieht man sofort, was Sache ist. Untersucht wird, welche Änderung ${\rm{d}}{\kern 1pt} y$ durch eine Änderung ${\rm{d}}{\kern 1pt} x$ ausgelöst wird. Teilt man diese beiden Größen durcheinander, dann weiß man, wie stark sich $y$ (näherungsweise) ändert, wenn $x$ um eine Einheit erhöht wird.